Imputing and aggregating data

Note

For a more thorough explanation of how imputation works in the SHRUG, including visual and numerical examples, please follow this link.

When aggregating data to larger geographic units like districts and constituencies, or even simply incorporating a dataset at the shrid level, a constant challenge is dealing with missing and unmatched observations. Village and town match rates to the Economic Census range from 65% to 90%. Further, many Population Census fields are missing for some villages, especially in the village directories. Naively aggregating spatial units with missing data will result in undercounts of population and employment. Thus, we use a consistent algorithm to impute missing values where a suficient share of data in the aggregate unit is nonmissing. Then we set aggregate values that could not be imputed to missing.

Mapping	Depiction	Description	Weight Required
One to one (1:1)		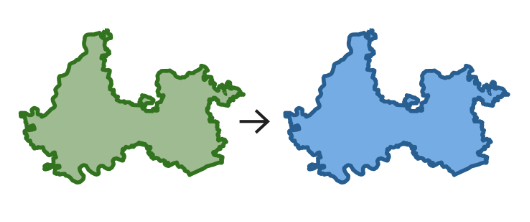A single unit from the source dataset maps to a single unit in the target identifiers	Required, must exist for the source units
Many to one (m:1)		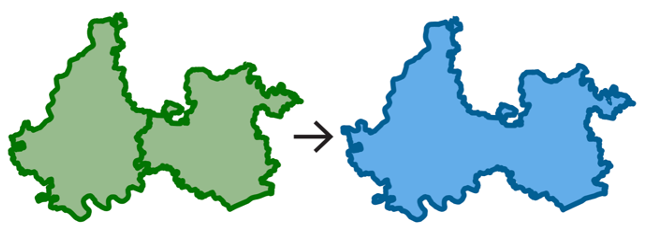Simple merge: many units from the source dataset merge to form a single unit in the target identifiers	Required, must exist for the source units
One to many (1:m)		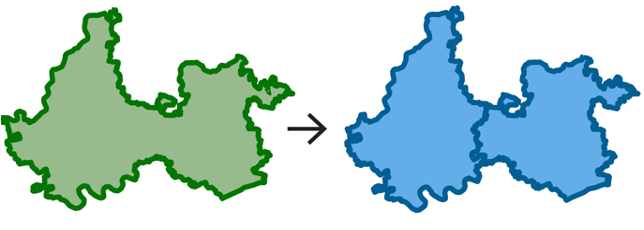Simple split: a single unit from the source dataset is split into many units in the target identifiers	Required, must exist for target units
Many to many (m:m)		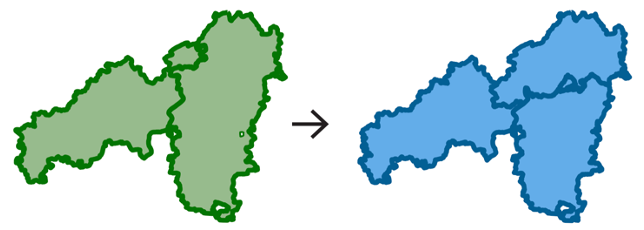Complex split/merge: many units from the source dataset merge and split to form a new set of many units in the target identifiers	Required, must exist for both the source and target units; OR must exist at a finer geographic resolution than the data.

Below we provide detailed description of the imputation logic. This approach provides what we think is the most accurate representation of the underlying data, e.g. of constituency growth over time. Undoubtedly some error is added by the imputation process, but these errors are likely to be smaller in importance than the noise that would be caused by treating missing towns and villages at zeroes in some years and not in others.

The use of weights in imputation

During imputation and aggregation, variables in the SHRUG are weighted by an appropriate variable. This is usually either population or land area, but not always, e.g. household asset variables in the SECC are weighted by SECC household counts. Population-weighted variables are expected to scale more closely with population (e.g. number of schools), and similarly land-weighted variables scale with land area (e.g. acreage of irrigated land).

Imputation weights are required for two reasons. First, they are required to determine whether a sufficient share of data in the aggregate is nonmissing. For example, if employee count is only known in villages representing 15% of the district's total population, then imputing values for the remaining 85% based on 15% is overly speculative. Throughout the SHRUG, we use 80% as the minimum proportion (by weight!) of the supergroup that must have nonmissing values in order to be imputed. Second, for count variables, weights are necessary to impute missing values (described below).

Source weight imputation

There are occasionally scenarios where the weights themselves will be imputed. For example, when weighting household asset variables in the SECC by SECC household count secc_hh, there are instances where certain PC11 villages and towns have missing values for secc_hh. In this case, we apply the same imputation method and 80% threshold to fill in those missings, weighted by PC11 PCA population pc11_pca_tot_p.

Imputation logic by variable type

In each case, to impute missing values of sub-units in aggregate unit A, we use the nonmissing values of the variable in the aggregate unit.

Count variables: Example: number of hospitals Weight: population Logic: Assume that the number of hospitals per capita in missing villages equals the aggregate number of hospitals/capita in all non-missing units.

Mean/median variables: Example: literacy rate Weight: population Logic: Assume that the missing value is equal to the population-weighted average of all nonmissing values in A.

Minimum/maximum variables: Example: Minimum temperature Weight: Not applicable Logic: Assume that the missing min/max value is equal to the min/max of nonmissing values in A. We treat indicators as maximum variables.

Imputation of weights (population and land area) in SHRUG's PC91-01-11 backbone

In the PC91-01-11 backbone of the shrid identifier, we link all the PC towns/village from each year to a shrid. To incorporate new datasets into the SHRUG, it is crucial to know how each PC town/village fits into its corresponding shrid. In the simplest case, a single PC91 village matches to a PC01 village matches to a PC11 village matches to a shrid. This is a one-to-one correspondence. However, PC town/village boundaries changed across years, and shrids are designed to be constant geographic locations between 1991-2011. This creates the more complicated case, in which a single shrid pools multiple PC towns/villages, in one or multiple years.

To handle shrids containing multiple PC units, we need a measurement of the relative importance of each PC unit in the shrid. Consider the extreme example in which a PC11 town with 1 million population is combined with a village of 500 population into 1 shrid. If we were given the literacy rate in the town of 0.8 and village of 0.2, and wanted to estimate average literacy rate in the shrid, we should not take a simple average. Instead, we want to account for the fact that the population of the town is much larger, so its literacy rate should have a much higher weight in the average. We can also see the need for weights when translating from shrid to individual PC units. If we are told that the shrid contains 20 hospitals, we should not assume an even split wherein the town has 10 hospitals and the village has 10 hospitals. Again, we should consider population as a weight. We use PC town/village population and land area as the two important types of weights.

The examples above highlight the need for weights generally. To integrate new datasets into the SHRUG, it is critical that every PC town/village, in every year, has a nonmissing value for population and land area. Some PC towns/villages are missing these values because they did not merge with the PCA (data source for population) or the town/village directories (data source for land area). We use the following strategies to impute missing weight values from nonmissing values.

Strategy for imputing missing population across PC years

Imagine that a PC11 village is missing population. We use the following rules to try to estimate a nonmissing population for that village.

1. Assume that within the same shrid, the average population growth rate of villages is the same. In practice, we calculate the total nonmissing village population in the shrid in 2011, then calculate the total nonmissing village population in 2001 or 1991. From these totals, we calculate the rate of change, and assume the same rate of change applies to the village with missing population.
2. The same is true for missing town populations. Assume that, within shrid, average population growth rate of towns is the same.
3. Order of imputation:
4. Use 2011 population to impute missing values in 2001 and 1991
5. Use 2001 population to impute missing values in 2011
6. Use 1991 population to impute remaining missing values in 2011
7. Use 1991 population to impute remaining missing values in 2001.
8. Use 2001 population to impute remaining missing values in 1991.

Important selection rules:

1. We use the PCA (Primary Census Abstract) for initial values of town/village population in every census year. We merge the PC91-01-11 shrid key to each urban and rural PCA.
2. We decided that, to be included in the SHRUG, a town/village must have a non-missing PCA population for at least 1 PC year. In other words, if a town/village was missing population after imputation, it was dropped. This results in a PC91-01-11 shrid key with no missing population.

Results from imputing population

This section describes the number of towns and villages we dropped because of Selection Rule 2, and the reason why we feel justified in dropping them.

Towns: After imputation, we’re missing population data in 0 PC91 towns, 34 PC01 towns, and 3 PC11 towns, but that seemed like an acceptable amount of error. These were dropped.

One source of confusion at this stage was the role of “outgrowths”. Outgrowths are urban areas connected to a census town. Together, outgrowths and towns form urban agglomerations (UA). For example, “New York City” is a UA, and “the Bronx” is an outgrowth. During the SHRUG1 build, we were worried that the census recorded some areas twice by including 1 row for the whole UA, and 1 row per outgrowth. In short, we retained outgrowths in the urban PCA (for 91, 01, 11), so the towns missing population are not due to dropped outgrowths.

Villages: After imputation, we were missing population for 51,513 PC91 villages, 46,132 PC01 villages, and 42,669 PC11 villages. These were dropped. Villages were dropped for 2 main reasons: 1. Villages with 0 population in the village directory. 2. Villages that were in the PC keys, but not in the PCA.

Our assumption was that villages were dropped from the 2001 and 2011 PCA if they had 0 population or other anomalous values, but would still be in the village directory. PC01 and PC11 can be explained by cause 2, since the number of villages missing population corresponds closely to the number of villages in key but not in PCA. However, in the 1991 rural PCA, there were 47k villages with 0 population.

Villages missing population after imputation (all were dropped):

• PC91: 51,513 villages
• 2,459 villages in the SHRUG keys but not the PCA. That means that ~48k villages are unexpectedly missing population.
• 47k had 0 population in the PC91 rural PCA.
• 515 were in the SHRUG but not the VD
• PC01: 46,132 villages
• 11% were in the SHRUG but not the VD
• 84% had 0 population in the VD
• PC11: 42,669 villages
• 0.1% were in the SHRUG but not the VD
• 99.8% had 0 population in the VD

Strategy for imputing town/village land area across PC years

Our goal is that every town/village should have a nonmissing land area, which will be used as one of the weights for merging new data into the SHRUG. There are 2 sources for land area data. Only PC11 has polygon geometries (i.e. a map of towns/villages from which we can calculate land area), so we focus largely on improving the completeness of PC11 land area.

Source 1: Ideally, we want to use the PC11 town/village directories for town/village land area. But the TD/VD land area variables are incomplete (some are missing) and others seem to be errors (e.g. 20k towns/villages have a land area of 0). These errors are not surprising, since the TD/VD land area variable was filled by asking a local bureaucrat to guess the settlement’s area, rather than from underlying geographic data.

Source 2: To fill in the missing and excessively low TD/VD area, we can calculate area using the the PC11 shapefile. While we have observed some systematic bias between the data sources, we have concluded that it is pretty safe to mix TD/VD and both polygon areas where needed.

Rules for imputation:

1. Use the town/village land area from the TD/VD whenever possible.
2. Eliminate villages in the VD that we think have erroneously small land area. That is, treat villages with land area in the VD below 0.1 square kilometers as missing for imputation. This applies to PC91, 01, and 11. a. We graphed the frequency of the smallest locations (bottom 10% of land area) of the TD/VD and polygon town/village areas. The rationale was that the TD/VD would have a bunch of areas that were too low, and at a certain point frequency in the VD and the polygons would begin to line up. Based on this graph, this point was 0.1 sq km. This is our bottom threshold, meaning that if a PC11 TD/VD land area was < 0.1 sq km, it is considered an error, and the land area weight is filled with polygon area instead.

3. Fill in missing PC11 land area using the shapefile.

4. Use PC11 land area to impute missing land area in the PC01 and PC91. The rule for backward imputing land area is based on the assumption that within the same shrid, land area does not change across census years. This rule is fairly simple, but consider a situation where you have a shrid with 3 villages, and you know the total shrid area, and land area for 1 village. E.g. you know the total shrid area is 20 sq. km., and the area of B1 is 5 sq. km.. How do you distribute the remaining 15 sq. km between B2 and B3? a. Our answer: a village-level weight, to estimate B2 and B3’s relative importance. For our imputation, we use village population. That is, if B2’s population is twice as large as B3’s, then we assume B2 has aland area of 10, and B3 has a land area of 5.

Note: unlike for population, we allow the SHRUG to have locations with missing land area. Results from imputing land area:

Results from imputing PC01 and PC91 from the PC11:

• After imputing PC11 land area: 57 villages and 27 towns that still don’t have a land area value. These will have a missing value in the SHRUG, and we will not be able to merge variables weighted on land area for these shrids.
• After imputing PC01 land area: 43 PC01 town rows and 445 village rows were missing land area.
• After imputing PC91 land area: 24 PC91 towns and 10,804 village rows were missing land area.

More information

In the metadata pages of this documentation website, you will find summary statistics that describe the degree of imputation that has taken place for each dataset. For more information, please reach out to info@devdatalab.org.